sinとcosの基本公式
数学でも物理でも公式と呼ばれるものはたくさんありますが
そのうちのかなりのものは、そのベースにある考え方をよく理解すれば、暗記が必要のないものです。
以前記事にしたことがありますが、特に物理については
得意な人やそれを専門に研究しているような人が決まって口にするのが
「公式なんて1つか2つ覚えておけば、あとはそれの応用だよ」というセリフです。
私などは到底及ぶところではありませんが、これは一つの真理を示しているものであると思います。
今回は三角比の基本公式について、このことを示してみたいと思います。
cosはxを示し、sinはyを示すことがベース
以前これも記事にしましたが、
三角比のcosは座標平面上のxを示し、sinはyを示します。
またtanは傾きを示します。
このことをよく理解しておけば、三角比の基本公式は暗記せずとも頭にすぐ浮かべることができるようになります。
三角比の一番基本の公式は tan= 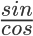 ですが
ですが
これはtanが座標平面上の傾きであることを理解しておけば
cos=x(この公式ではxの増加量)、sin=y (yの増加量)ということから、暗記などしなくても自動的に頭に浮かべることができます。
*単位円という縛りがあるため x、yともに最大で1までの範囲での話になるので、x,yとxの増加量とyの増加量がここでは同じになります。思い出しやすくするため単にx,yとして単純化した方が記憶が復帰しやすいでしょう。
もちろん中学で学習する関数の基本である
[ 変化の割合= yの増加量 / xの増加量 ]という公式は知っている必要がありますが
実はそもそもこの公式も、ここでは詳しく説明をしませんがグラフの仕組みを知っていれば暗記など不要の物です。
三角比や三角関数の問題で最も使われる公式もこれでOK
非常に有名で、さまざまなタイプの出題に最も使われる基本中の基本公式として
sin2Θ+cos2Θ=1という公式があります。
この公式を単純暗記しようとして、他の公式が色々出てきた際にそれらと混ざってしまって結構混乱する生徒が多いのですが
この公式こそ覚える必要がない公式です。三平方の定理を知っていれば、いつでも一瞬で頭に浮かべることが可能です。
sin=y,cos=xという原理を知っていさえすればOKなのです。
説明しますね。
三平方の定理を考える際に、直角三角形の2辺をx,yとした場合には
斜辺2=x2+ y2ということになります。
そしてここでいう斜辺は、三角比では単位円の半径rにあたります。
また単位円の半径rは1ですから、斜辺は1であり斜辺2も1になります。
したがって12= x2+ y2 であり、 sin=y,cos=x ならば当然に
sin2Θ+cos2Θ=1 という式が導き出されることになります。
何のことはない、単に三平方の定理を三角比に流用しているだけのものだったのです。
そして三平方の定理もさすがにピタゴラスだけあって、証明を要さない、真の法則中の法則という感じがしますが、
これとても、直角三角形に正方形をくっつけた図を頭でイメージしておけば、覚える必要なく思い出せると思います。
高等数学で暗記する所は別にある。
このように高校の数学で登場する公式の多くは(中学の数学もですが)
暗記など不要で定着をさせることができます。
今回の公式は単に一例ですが、言い方を変えると
単純暗記では高等数学は乗り切れないと言っても良いかもしれません。
その背景にある理論と結び付けた考え方が重要なので
それを軽視して単に字面のみ覚えても、有機的な知識の塊になっていないためすぐ忘れてしまいます。逆に非効率です。
考え方を追っていくとおそらくどの分野でも、このような暗記を不要とする理解定着が可能な部分がかなりあるので、それを見つけ出すことが肝要かと思います。
しかし逆に暗記をした方が良いところもあります。
それは公式ではなく、問題解法の切り口です。
これについては以前から何回も記事にしていますので、そちらを参照していただくとよいですが、
たとえば、チャートの膨大な問題を1つずつ解いていくというスタイルで高校の数学の学習を進める場合、
ある程度進めてきて(最低1回通ったら)もう計算などは飛ばしてしまって、問題の解法の切り口を暗記することが重要になります。
それによって時間節約ができる上、たとえば野球で言えばバッティングフォームを体でマスターするような基礎を作り上げることが可能になります。
ここを二回目三回目になるのに、ひたすら一から問題を解き計算もしっかりやって答えを出し、確認を丁寧にやっているようだと、
「いつまでも全体像がつかめず得点力がつかない」という状況に陥ることは、多くの生徒の実例を見ていると必至の結果だと言えます。
そのような事態を避けるために
公式は背景をよく学び、「暗記ではなく理解」によって頭に入れておくようにして
問題の解法は、ある程度進んだら、「理解でなく暗記」によって定着を仕上げるようにする
これが必勝のパターンだと思います。
今後も皆さんのお役に立つ情報をアップしていきます。

