クォーター(quarter): 意味 4分の1のこと
それ、筆算でやるの?
単純な計算のコツはいろいろあります。
最近では、人によっては大学生くらいでも、計算は全て筆算でやるという人がいます。
普通にスマホの電卓があって使える時代にはなったので
自分で計算をする機会が減ってきていることもあってかもしれませんが、
それでも暗算をする場面は、実際結構ありますから、省力化をしたいものです。
ましてや勉強の際の計算については
テストの際の時間節約になりますから、計算法は意外に重要です。
計算のコツにはいろいろありますが、たとえばクォーターの数(4分の1)を使った25を活用した暗算などは大変便利です。
たとえば、100の4分の1が25であることを利用して、25×4を暗算で100と求めることができます。
さらに200なら、その2倍なので25×8=200になりますね。
50の半分が25で、25が4つ集まって100になっているというイメージを持つと、それが2セットになったのが200と考えることができ、わかりやすいです。
25という数字を活用するやり方は、小学校の計算の工夫の単元などにも出てくる考え方です。
これにはさらにいろんな利用法があります。
まず、25の倍数は暗算で出せるようになります。
25×5=125 というのも、25が4つで100、それにもう1つ25があるから125
というイメージで暗算ができます。
さらに逆の5×25が出てきた場合も、25の存在に気づけば、
25×5にして暗算できてしまいます。
25だけでなく、75のような25の倍数も、100の4分の1が3つだから4分の3というイメージがあれば
たとえば、小数で0.75×4というような問題が出てきても 、4分の3 × 4=3という形にして簡単に計算ができます。
小数でない場合には、たとえば、75×4なら(25×3)×4と考えて、これも25をベースにして順番を入れ替えて(25×4)×3=100×3=300で答えを暗算で出せてしまいます。
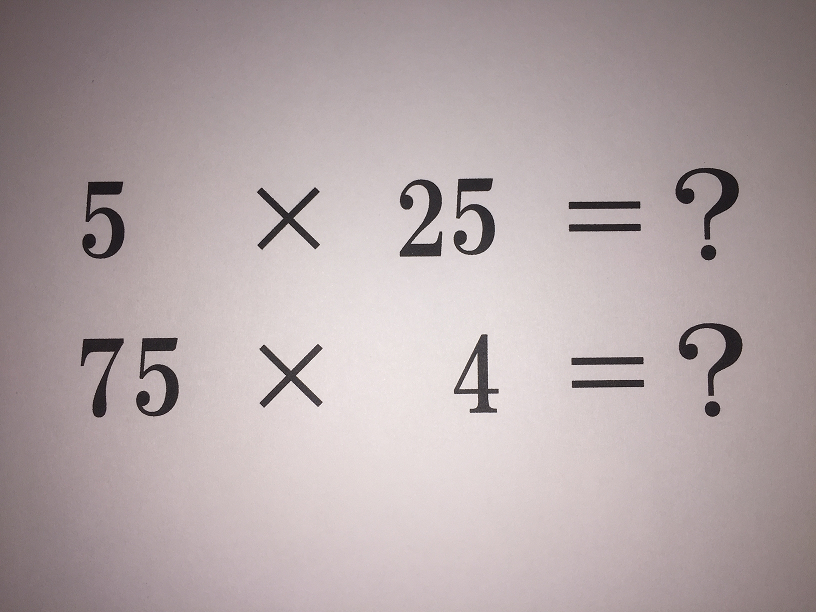
クォーターの数のようなやや高度なコツでなくても、
たとえば、24×2000のような計算で、24×2を計算したら、あとは0を3つくっつけておけばいいとか
×0.5は半分にすればいいというようなのも、コツといえばコツになるでしょうか。
このように単に計算といってもいろいろ便利な方法があって、指導の際に教えたりします。
しかし、これらはいわゆるコツですから、もちろん使わずに1から10まで筆算したって答えは出ます。
楽してもいいんだよ。
さて、本題に入ります。
このようなコツを生徒に教えると、だいたいの生徒はその時は納得をして、そのやり方で計算をします。
しかし、1週間位経って同じような計算をするときにはその行動は2つに分かれます。
1つ目のタイプは、そのやり方を使って計算をする生徒です。
あたり前と言えばあたり前の反応です。教えたのですから…。
けれども、もう1つのタイプの生徒が確実にいます。
それが、再びすべてコツを使わない筆算で計算をする生徒です。
24×2000であれば、ていねいに0をかける段まで作って計算をしていたりします。
400×0.5を一生懸命筆算にして、しかも小数点を忘れてミスをしたりしています。(答えは、400の半分だから200ですね)
そして教師は心の中で叫びます。 「何で?」
以前は不思議でしたが、最近ではあまりに多く見かけるので驚きません。
高校生でも、このような計算をする生徒がわりといます。
コツを学んでも「ふーん、そんな方法あるのか」と思うだけで、
それを自分の方法として使おうとはしないんです。

何だか、より簡単な方法や便利な方法を避けて、敢えていばらの道を進んでいるかのようです。
たとえば、便利なスマホを使わずガラケーを使ったり、旧式の車に乗ったりする行動にはポリシーや別のメリットがあるかもしれませんが
計算のコツを知っているのに敢えて使わないことには、そのようなメリットはありません。
そして、そんな生徒から、「先生、計算に時間がかかってテストで時間不足になった」という報告があったりします。
「あたり前だよ」 私はまた心の中で叫んでしまうのです。
「使っていいんだよ。計算のコツ」
そんな事を一人つぶやきます。
便利なものがすべて良いとは言いませんが
自分にメリットのあるやり方は吸収して、今までのやり方を常に変えて進化させていく、
そういう意識が持てる人と持てない人との差は、長い目でみると大きなものになるのかもしれません。
「変化を恐れず進む」
この言葉は、身近なこんな計算のコツのようなものの学習にも必要なのでしょう。
今後も皆さんのお役にたつ情報をアップしていきます。

