さか上がりと割合の計算
小学校の高学年の算数で一番の難所と言ってもいい割合の計算ですが、一度コツをつかめばそんなに複雑ではありません。
しかしコツをつかむまではいつまでも延々とできなくて苦しむことになる単元だと言えます。
さか上がりの練習と似ています。
コツがあるのですが、力押しでやるとなかなかうまくいかないのです。
もちろん公式を覚えていき、それを式に当てはめる形を覚えていくという過程をやっていくという作業は当然必要です。
でも多くの生徒は、それを一通りやった後必ずと言ってよいほど再び軽い混乱に陥ります。
生徒によってその程度は異なりますが、混乱がひどいともう一度一からやり直さなくてはなりません。
混乱する理由
以前割合のことを記事にしてそこでも書きましたが、http://wizzseiun.com/2019/10/13/percentage/
割合の勉強をするときに公式をただ数値として頭の中で組み合わせて計算をしてしまっている場合が非常に多くあります。
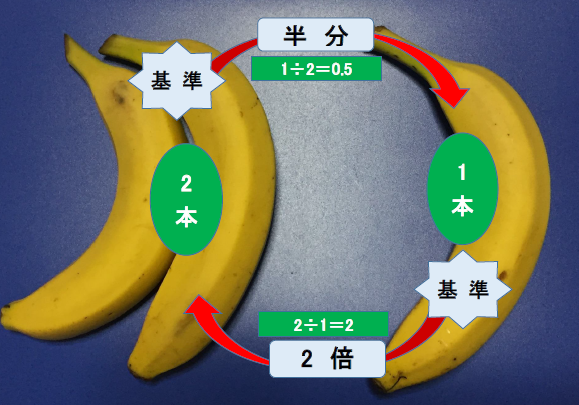
①100人と比べて125人はその何倍か?
②125人を1としたときの100人の割合は?
と出題されたとき、
非常に多くの生徒が
①も②も何となく
①125÷100=1.25倍 ②125÷100=1.25 とか
①100÷125=0.8倍 ②100÷125=0.8というように
同じ答えを書きます。
これは算数が得意な生徒も同じです。
学習直後でなく、しばらくして出題された場合には、
自信をもって
正答 ①1.25倍 ②0.8
を書ける生徒は本当に少ないと思います。
この二つの問題に同時に正答が出せる状態が「コツをつかんだ」状態で、
さか上がりで言えば、上手く腰を折り返すポイントをつかんだところになるでしょうか。
なかなか、つかめそうでつかめないポイントだと言えます。
イメージができていないことが最大の問題
ではそのコツの正体は何かと言いますと、
「比べる」という意識を持つということです。
割合の学習は、二つの数量を「比べる」計算の学習なのですが、ほとんどの生徒はそのことに気づかないか、そのことを見失っています。
「比べる」のですから当然大小があり、
「もとになる量(基準になる量)」に対して「比べる量」がどれくらいなのかを確認するためのバロメーターを創ろうということで考えられたのが割合なのですから、
「『基準』と比べてどれくらいか」ということを、大小を意識して考えることが圧倒的に重要なのです。
①の問題では、「基準」は100人で
それと比べて125人はどれくらいかを聞いているので、比べる方が大きいのですから、
出てきた答えが1より大きい1.25にならないとおかしいのです。
0.8は基準より小さいことを示す数字です。
②の問題では、「基準」は125人で
それと比べて100人はどれくらいかを聞いているので、
比べる方が小さいので0.8が正しいことになります。
そうです。
実際に「どっちが大きいのか」「どっちが小さいのか」
「この問題ではどちらを基準にして聞いているのか」
この単純なイメージが実は非常に重要なのです。
割合を得意にしている生徒に、
「どっちを基準にして計算するの?」と聞くと
正しい方を即答します。
曖昧な答えをする生徒は、まだ必ずミスをします。
だから割合を特にするコツは、このイメージをする力にあることは間違いないと思います。
問題を解くたびに、「基準」になる量の所に○をつけて意識する習慣をつけるのもいいかも知れません。
また、混乱してしまった場合には、まず適当に100÷125 125÷100をやっていって、その後に「えっと、どっちが大きいのだろう」と確認して問題にあっている答えを選ぶというようなやり方もあります。
こういうやり方は学校では「適当なやり方だから公式をきちんと覚えなさい」と言われてしまうかも知れませんが、大小の比較のイメージができない場合にはかなり有効です。
慣れないうちはそれも一つの手かも知れません。
割合の学習をする場合は、公式を覚えていくことも大切ですが、このようなイメージ力が実は決めてになります。
割合の学習は「比べる」学習だという大本を意識するということとも言えるかもしれません。
今後も皆さんのお役に立つ情報をアップしていきます。