苦手意識を持ちやすい「割合」の学習
小学校に算数で苦手な分野を聞いたら、おそらく多くの生徒と保護者が「割合」と答えるでしょう。
これには理由があります。
それは、公式のアイテムになる「もとにする量」、「比べる量」という言葉の意味がつかみにくく、問題文からそれを読み取ることが国語的な意味で難しいと感じられてしまうからです。
「〇〇を1とすると」「〇〇をもとにして」という言葉の意味がこれまで出てきた算数の用語と比べて、急に概念的で抽象性が高いため、通常の小学生はかなり戸惑います。
実際わかりにくい言葉だと思います。
簡単にいうと「〇〇を基準として、これを1という数にして考えてみると」ということなのですが
「基準」という言葉がまだ難しいため、「もとにすると」とか「1とすると」という表現を使っているのだと考えますが、かえって難しく感じるのは私だけでしょうか。
とにかく割合の学習については、冒頭から「何かぼやっとしていてわかりにくいな」という印象を生徒は受けるようです。
いったい何を学習しているのかを理解する
そもそも、「割合」ってどういうことなのか、それがはっきりわかって問題を解けている生徒は実は少ないと思います。
最初に「もとにする」という話が来てよくわからないところに、公式が出てきてすぐ計算問題になっていくため
何をやっているか十分に理解していないうちに、何となく計算のきまりだけ覚えようとします。
「割合」は、小数や分数をともなった割合という形の単元で、学年が変わると再び出てくるのですが、再度出てきたときには、優秀な生徒でもほとんど忘れかかってしまっていることがあります。
これは、最初にベースとなる考え方の部分をしっかり理解しないで進んでしまうやり方が大きな原因だと思います。
「割合」というものは、二つの数値を比べる際に、どれくらい違うかを表すために考えられたものです。
そして、比べるのですから、どちらかを基準にします。
そして基準があるということなので、比べる相手がその何倍になるかということが問題になります。
すべてのスタートはここにあるということを、まず十分に生徒が理解する必要があります。
二つの割合があること、これが混乱のポイント
何となく数字を組み合わせて答えを出すことに慣れている生徒が混乱するポイントは、二つの割合があることです。
二つの数値を比べるのですから、比べ方で2通りの割合が出るのは当然ですが、生徒はどちらを出せばよいかわかりません。適当に一方を書いてすべて×などということもよく見かけます。
10÷2なのか2÷10なのかが一向にわかりません。
これは「基準」がどこにあるかをしっかり考えずに計算をやっているため生じるミスです。
要は「割合」が何かを知らないまま、公式を覚えても役に立たないということになります。
非常の多くの生徒が「割合」が苦手な理由は、実は、公式がうまく適用できないとか、パターンが定着しないということの前に、まず「割合」と「基準」ということ自体の意味がつかめてないことにあるのです。
割合を得意に変える方法
では、混乱しがちな「割合」を逆に得意に変えるためには。
それにはまず、「割合」の考え方をしっかり頭にいれることが重要です。
たとえば、ジャイアンがバナナを2本食べ、のび太がバナナを1本食べるとします。
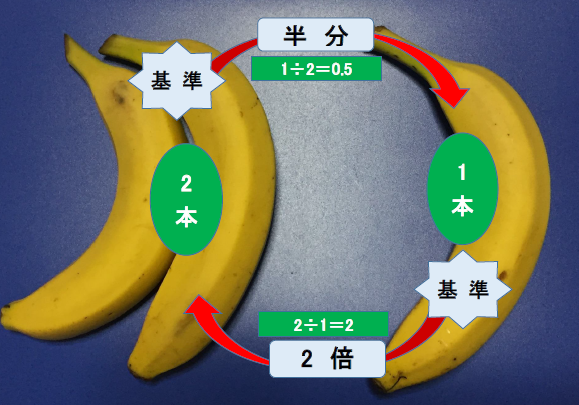
①のび太のバナナの本数を基準にすると、ジャイアンは2倍あります。
②この時に、ジャイアンのバナナの本数を基準にすれば、のび太は半分しかありません。
これが「割合」です。そしてこれだけの話です。
半分=0.5=2分の1 ということだけ別に理解しておけば、公式を覚えなくても、これらの文章だけで割合の計算はできてしまいます。
①では1本ののび太が基準(もとにする量)で、2本のジャイアンをそれと比べました(比べる量)。それで出てきた数値である、「2倍」というのが「割合」です。これを覚えておけば、いつでも割合は計算できます。
何かを基準にして、ほかの何かを比べるとき、比べる方の数を、基準になる方の数で割ればよいのです。
基準の数を聞かれたり、比べる方の数を聞かれたりする場合にも「どうやったらほかの数の計算で、のび太の1本が出せるかな。どうやったらジャイアンの2本が出せるかな」とこの話を振り返るだけで出せます。
どんな数値が出てきても、問題の書き方がいろいろ違っても、
基準が何で、比べているのが何かということをつかめていれば、別に公式として覚えなくても割合の計算は簡単にできるのです。
もちろん公式を使った方が便利なので、公式を否定するものではありません。
ただ、考え方がベースになくて公式だけ覚えても、それは役にたたないということを知る必要があると思います。ここがポイントです。
難しい単元だと思い、公式を暗記して練習を繰り返して一生懸命やっても、基本になる考え方をしっかり理解しないままやっていては、すぐ忘れるのも無理はありません。
思考をしない暗記的学習は後に残りにくいからです。
基本の理解というのはこういうことだと思います。
あと、答えを出したときに確認をする場合のコツとして、比べる方と基準の方が同じときが割合1(1倍)で、
比べる方が大きい場合は割合は1を超え、比べる方が小さい場合は割合が1より小さくなる(小数)ことを覚えておくと良いでしょう。
今後も、お役にたつ学習のコツを書いていきます。

