[mathjax]
平方根と累乗根
中3数学で平方根についての学習をします。
平方根と言うのは、次のようなものです。
たとえば2×2=4について、4は2を2回かけあわせたので「2の2乗」あるいは「2の平方」と言います。
平方根はこれと逆の考え方で、2回かけあわせると4になる数のことです。
2×2=4、そして(-2)×(-2)=4ですから
4の平方根は ±2ということになります。
整数で表現できない場合にはルートを使って表します。
たとえば7の平方根は整数が存在しないので、± 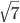 と表します。
と表します。
中学ではここまでですが
高校数学では、累乗根と言うことで3回かけあわせるとその数になる3乗根や
4回かけあわせるとその数になる4乗根など、それ以上の次数の累乗根も学習します。
たとえば2の3乗は8ですから、8の3乗根は2ということになります。
(*-2は3乗するとー8になるので、3乗根ではありません)
指数との関係
ところが高校数学では、別の方向からこの学習が始まります。
それが指数公式です。
ここでは平方根= 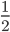 乗、3乗根=
乗、3乗根= 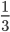 乗という考え方が登場します。
乗という考え方が登場します。
計算をするためにはこのことをそのまま使っていけばいいのですが
当然のことながら「どうしてルートが 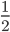 乗 になるのか」という疑問が湧きます。
乗 になるのか」という疑問が湧きます。
ほとんどの生徒がこのことを疑問に思うようです。
ただ解決しなくても計算には支障がないので、理由がわからないままの生徒はたくさんいるはずです。
学ぶ楽しさはこういうことから
しかしわからないままの公式をそのまま使っているというのも、なんだかピンときませんね。
こういうところで「ああそうか」ということができれば
学ぶ楽しさは倍増して、次へ進む際の原動力になるはずです。
だからこういうポイントを軽視しないほうが良いのです。
そして意外な場面で、どうしてそうなっているのかを知っていることが役に立つということもよくあります。
知識と言うものは一本線というよりも、複数の線が絡み合っているようなもので、どこかで有機的につながりを持っていて、それがつながることで有益なものになっていくものだからです。
平方根= 2分の1乗 になる理由
先ほどの4の平方根である ±2を例にとって考えてみます。
指数公式によれば、この ±2が4 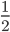 と言うことになります。
と言うことになります。
でも4を2回かけあわせるのは4×4=16で16になるのがわかりますが
2分の1回かけあわせるというのが、実際にどういう意味なのかは想像することができません。
直前の1乗、つまり「その数そのもの」についても1回かけあわせるというのが、どういうことなのか想像が困難です。
強いていけば、2回かけあわせるというのが実際にはかけあわせのスタートになるから
1回かけあわせるというのは「かけあわせない」という風に日本語的には考えることもでき、
だから「4のまま」とも言えるのでしょうか。
しかし分数になると、イメージは難しいですね。
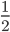 乗 は半分回かけあわせるので、逆に平方根の世界に入っていくという風にもとらえられますが、ちょっと難しいイメージかも知れません。
乗 は半分回かけあわせるので、逆に平方根の世界に入っていくという風にもとらえられますが、ちょっと難しいイメージかも知れません。
だとすると、これはやはり理論的に考えていくしかないようです。
このように考えます。
4の平方根の ±2は、当たり前のことですが、これをさらに2乗すると4の1乗である4に戻ります。
これを指数で考えてみます。
4の平方根は4 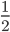 ですから、4の平方根を2乗したら元の4になるというのは
ですから、4の平方根を2乗したら元の4になるというのは
(4 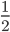 )2 =4
)2 =4 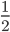 ×2 =41 =4
×2 =41 =4
という計算になります。(*計算は(Xm)n=Xmn の公式によります)
(±2)2=4と同じ結果ですね。
これは3乗根でも同じで 8の3乗根は 8 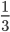 ですから、8の3乗根を3乗したらもとの8になるというのは
ですから、8の3乗根を3乗したらもとの8になるというのは
(8 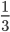 )3 =8
)3 =8 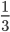 ×3 =81 =8
×3 =81 =8
という計算です。これも8の3乗根である2を3乗した(2)3=8と同じ結果です。
こういうことから、 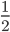 乗や
乗や 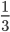 乗のような分数乗というものが、ルートと同じになるというわけです。
乗のような分数乗というものが、ルートと同じになるというわけです。
指数計算の学習は、やり始めるととても面白いですが
この分数上の考え方をよく味わってもらい、さらに学習の原動力にしていただけたらと思います。
今後も皆さんのお役に立つ情報をアップしていきます。

